二項分布
一定の時間内に1人の顧客が来る確率をpとすると、顧客が来ない確率は(1−p)となる。この時、顧客の総数がn人であるとして、そのうちのk人が実際に来るものとすればその確率は、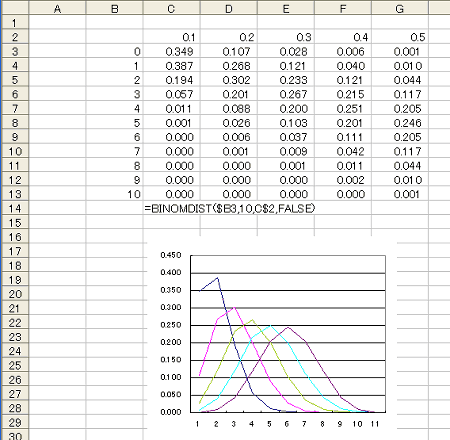
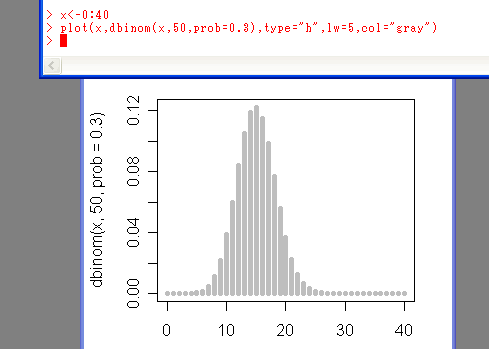
R による実行例
Pk=nCkpk(1−p)n−k
となる。
このように、結果が成功か失敗のいずれかである n 回の独立な試行を行ったときの成功数で表される離散確率分布を二項分布という。
nCkは二項係数と呼ばれ、 n 個から k 個を選ぶ組合せの数のことであり、
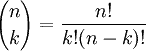
とも表される。また、二項分布でk回の場合の確率は、
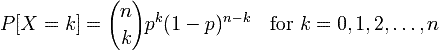
と表される。


R による実行例