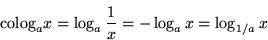|

|
- ...
\let
-
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 和集合1.1
- 集合 A と集合 B が与えられたとき,
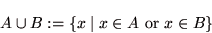 |
(1.1) |
として定義される集合を、集合 A, B の和集合という.集合 A, B が交わりを持たないとき、この和集合が直和(direct sum)と呼び,
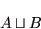 |
(1.2) |
と表現する.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 積集合1.2
- 集合 A と集合 B が与えられたとき,
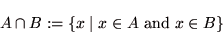 |
(1.3) |
を積集合という.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... で微分2.1
- 実関数 f(x) について極限
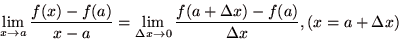 |
(2.10) |
が存在するとき 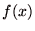 は は 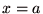 において微分可能(differentiable)であるといい、この極限を と書き において微分可能(differentiable)であるといい、この極限を と書き 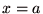 における における 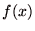 の微分係数という. の微分係数という.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ネイピア数を底とする対数2.2
- 一般に、対数とは任意の数
 を を 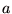 を底とする指数関数により を底とする指数関数により 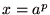 と表したときの冪指数 と表したときの冪指数 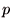 の事である.対数の概念は、16世紀末にヨスト・ビュルギとジョン・ネイピアによって考案された. の事である.対数の概念は、16世紀末にヨスト・ビュルギとジョン・ネイピアによって考案された. 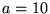 とした対数は常用対数(common logarithm)ないしはブリッグスの対数(Briggsian logarithms)と呼ばれる.常用対数は とした対数は常用対数(common logarithm)ないしはブリッグスの対数(Briggsian logarithms)と呼ばれる.常用対数は 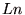 などと大文字を用いて表現する.また、 などと大文字を用いて表現する.また、
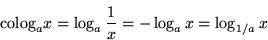 |
(2.20) |
を余対数という.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
|

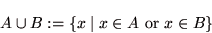
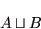
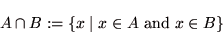
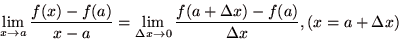
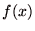 は
は 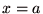 において微分可能(differentiable)であるといい、この極限を と書き
において微分可能(differentiable)であるといい、この極限を と書き 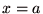 における
における 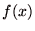 の微分係数という.
の微分係数という.
 を
を 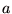 を底とする指数関数により
を底とする指数関数により 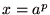 と表したときの冪指数
と表したときの冪指数 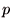 の事である.対数の概念は、16世紀末にヨスト・ビュルギとジョン・ネイピアによって考案された.
の事である.対数の概念は、16世紀末にヨスト・ビュルギとジョン・ネイピアによって考案された. 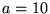 とした対数は常用対数(common logarithm)ないしはブリッグスの対数(Briggsian logarithms)と呼ばれる.常用対数は
とした対数は常用対数(common logarithm)ないしはブリッグスの対数(Briggsian logarithms)と呼ばれる.常用対数は 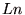 などと大文字を用いて表現する.また、
などと大文字を用いて表現する.また、